Adiabatic quantum computation
Unitary and dissipative dynamics of quantum spin systems for adiabatic quantum computation and shortcuts to adiabaticity.
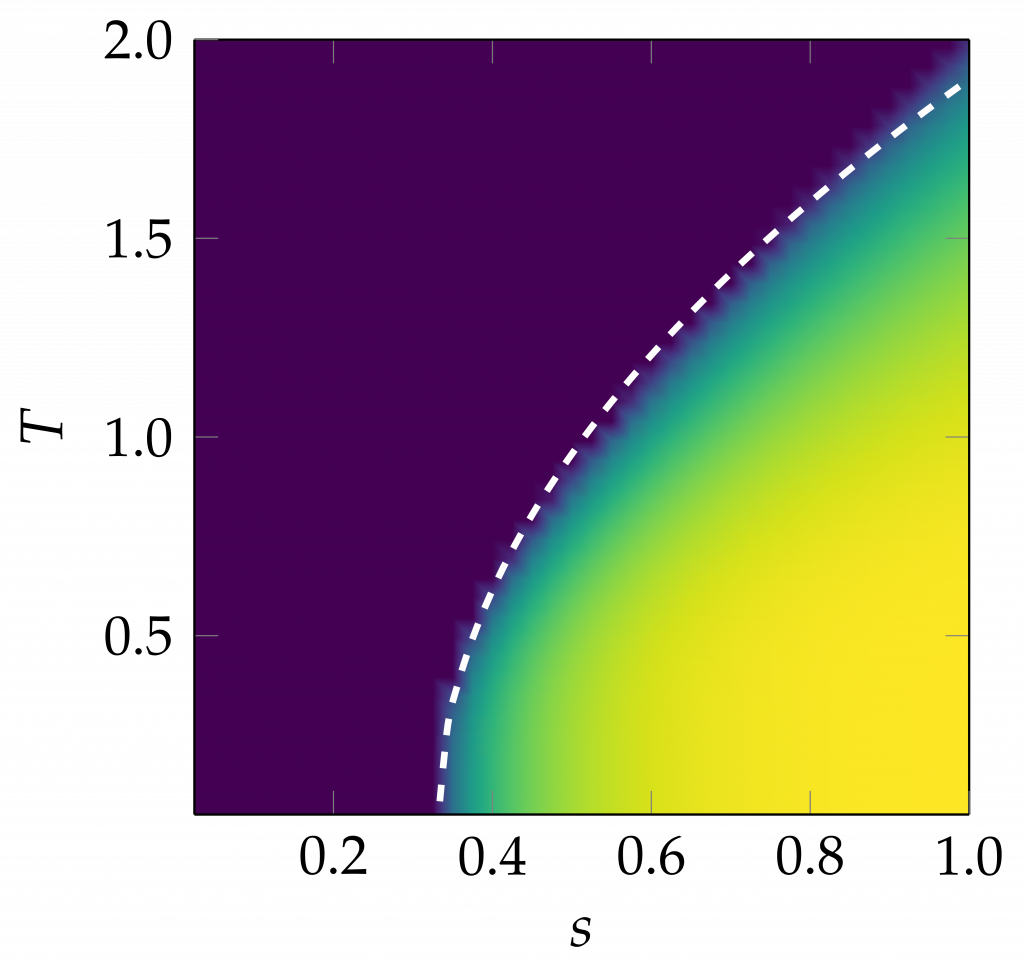
Quantum phase transitions in open systems
Quantum spin models with coupling to Ohmic heat baths of quantum oscillators. Nature and order of quantum transitions investigated combining state of art numerical techniques, among which Lindblad master equations (LME), Matrix Product States (MPS), Quantum Monte Carlo (QMC) methods.
Artificial intelligence for quantum computation
Design and optimization of quantum algorithms using machine learning and artificial intelligence tools.
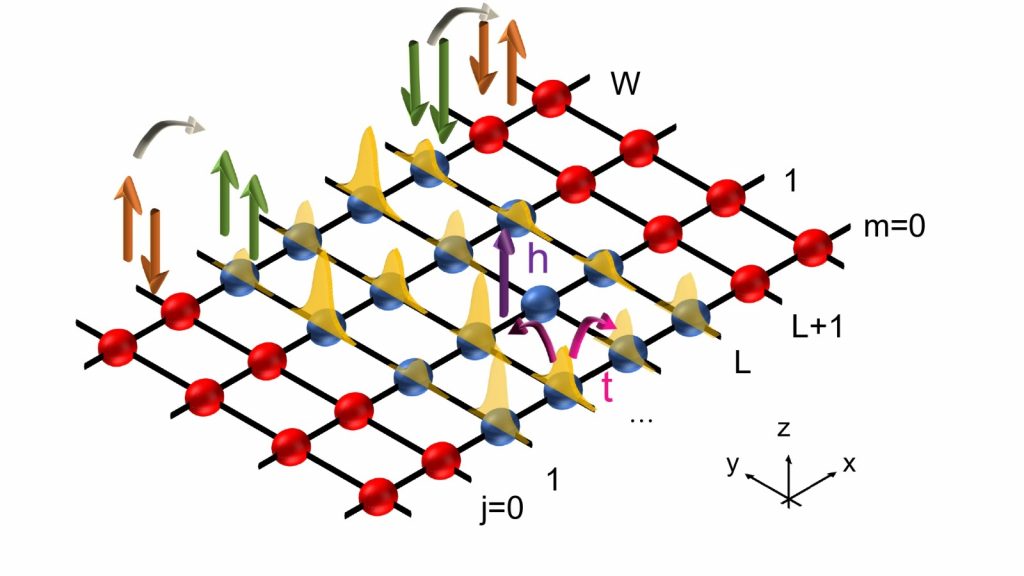
Quantum dynamics and thermodynamics of qubits coupled to leads and/or detectors
Heat and work transfers involving quantum systems embedded between leads with different temperatures and/or electrochemical potentials. Time monitoring of the qubit relaxation and decoherence by following the dynamics of coupled resonators acting as detectors in an external environment. Quantum efficiencies, noise and measurement back-action evaluated with different numerical techniques, such as variational approaches, exact diagonalization techniques, Non-equilibrium Keldysh (NEK) approach, LME and MPS method.
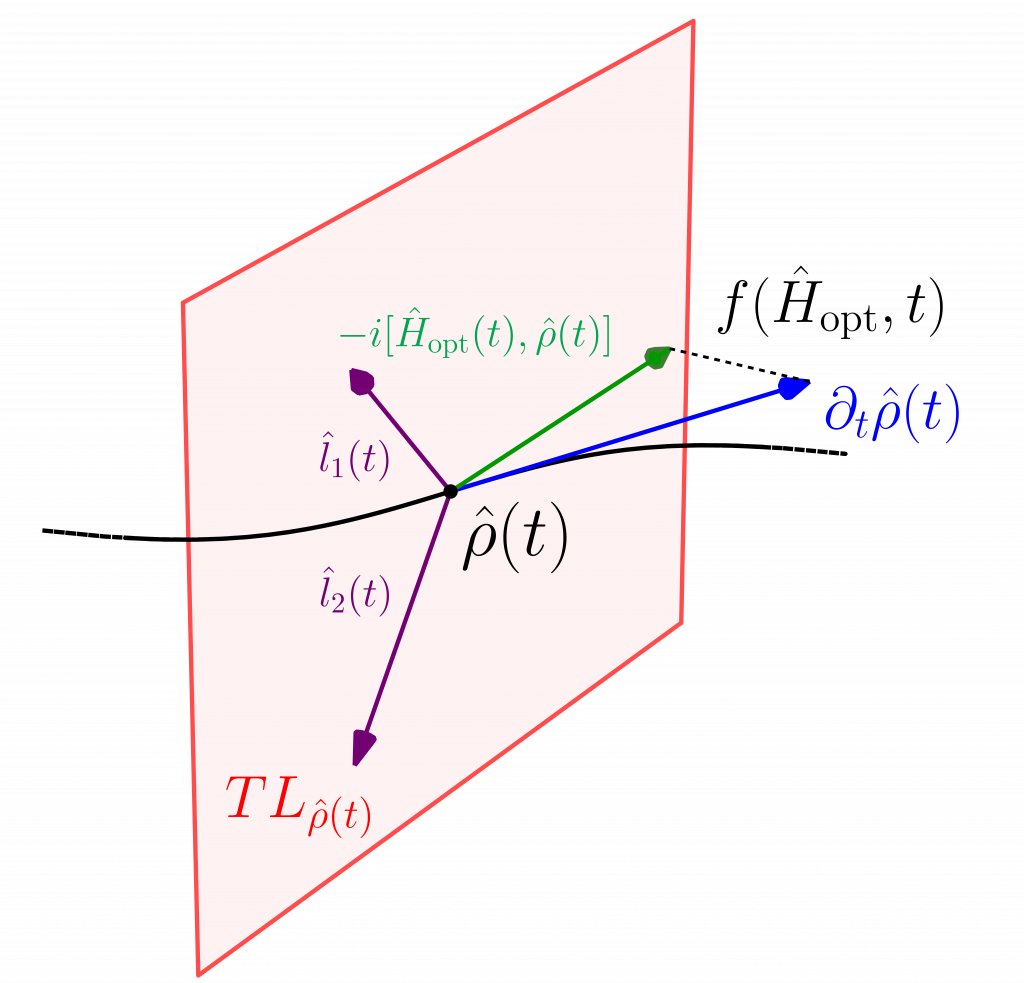
Hamiltonian learning and variational approaches
Study of parent Hamiltonians and for time-dependent and time-independent states. Quantum process tomography and variational approaches for digitized quantum optimization (QAOA).
Strongly correlated electrons in oxide bulks, interfaces and nanostructures
Numerical simulation of linear and non-linear response by electrons strongly coupled to phonons in oxide systems. Static and dynamic quantities evaluated by several numerical methods such as time-dependent Lanczos technique, NEK and memory function formalism.
Topological insulators and superconductors
Numerical calculation of topological invariants in Hermitian and non-Hermitian topological systems. Generalized Berry phase, winding number and polarization calculated by means of exact diagonalization techniques and cluster perturbation theory (CPT).
Theory of superconducting heterostructures for novel quantum devices
Lattice tight binding Bogolubov De Gennes approach to quantum transport using recursive Green’s function to characterize novel hybrid systems.